|
For more than 2,000 years encrypted communication required that the two communicating parties share a common secret--the
symmetric key used for encryption and decryption. One difficulty with this approach is that the two parties must somehow agree
on the shared key; but to do so requires communication!
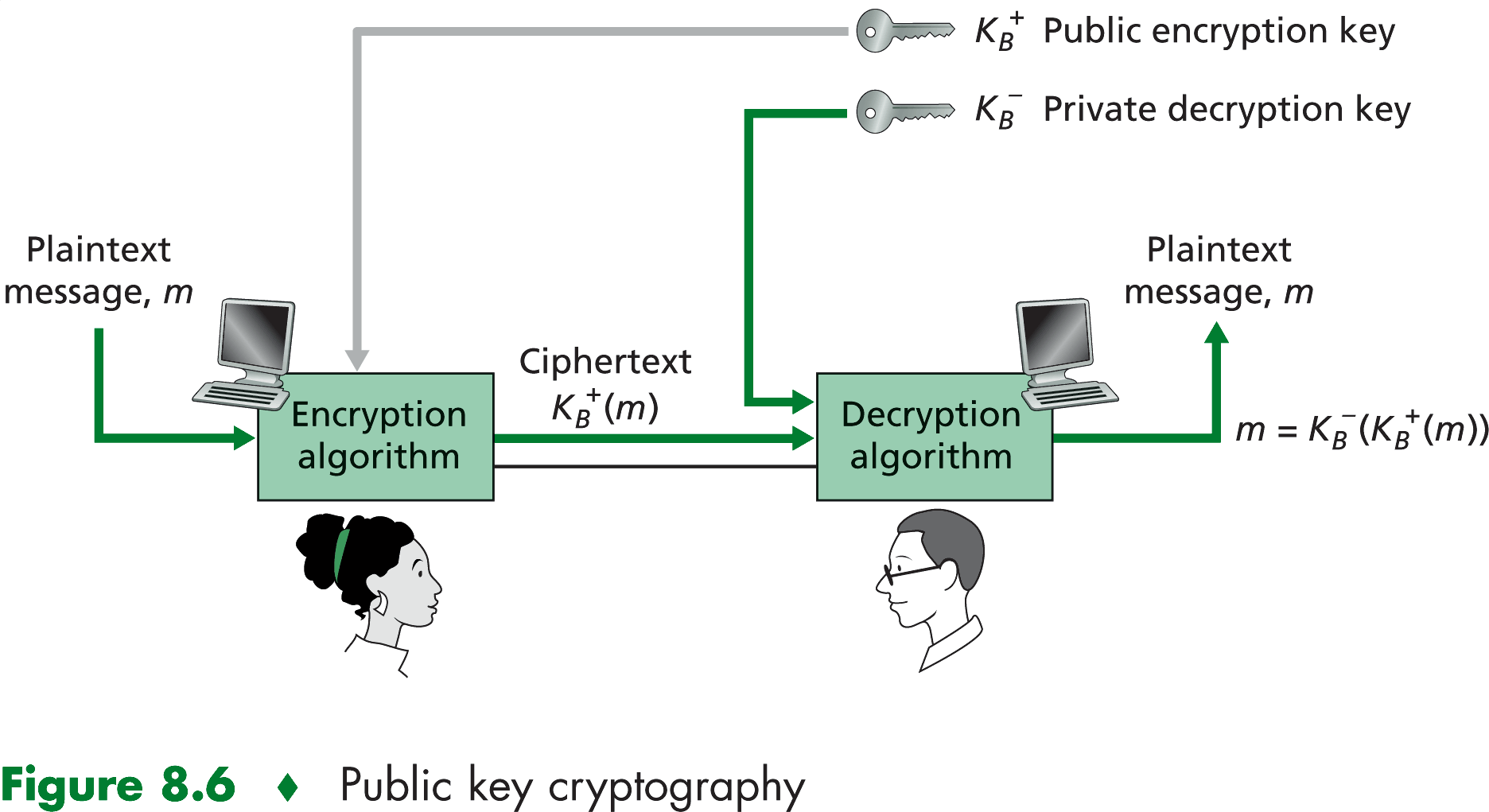
The use of public key cryptography is thus conceptually simple. But two immediate worries may spring to mind.
A first concern is that although an intruder intercepting an encrypted message will see only gibberish, the intruder knows
both the key and the algorithm that is used for encryption.
A second concern is that since an encryption key is public, anyone can send an encrypted message to someone claiming
to be you. In the case of a single shared secret key, fact that the sender knows the secret key implicitly identifies
the sender to the receiver.
While there may be many algorithms and keys that address these concerns, the RSA algorithm has becom
almost synonymous with public key cryptography.
There are two interrelated components of RSA:
- The choice of the public key and the private key.
- The encryption and decryption algorithm.
In order to choose the public and private keys, you must perform the following steps:
- Choose two large prime numbers, p and q.
- Compute n=pq and z=(p-1)(q-1).
- Choose a number, e, less than n, which has no common factors with z.
- Find a number, d, such the ed-1 is exactly divisible by z.
- The public key that you make available to the world, K+B, is the pair of numbers (n,e); your provate key, K-B, is the
pair of numbers (n,d).
|
